
Electric Distributors In Ontario
Prepared for Ontario Energy Board Staff
By F.J. Cronin, M. King and E. Colleran
PHB Hagler Bailly Consulting
July 6, 1999
Foreword
This report was prepared for Ontario Energy Board Staff by F.J. Cronin, M. King and E. Colleran of PHB Hagler Bailly Consulting and is the technical report referenced in Chapter 4, Rate Adjustment Mechanism, of the Ontario Energy Board Staff Proposed Electric Distribution Rate Handbook (June 30, 1999).
The report reviews the economic operating performance of the electric distributors in Ontario over the 1988 to 1997 period and estimates the change in total factor productivity and utility input prices.
The report also includes a discussion on the theory and evolution of price cap regulation, a review of methodology, assumptions, and data involved in estimating total factor productivity and input prices, and presents the empirical results of the analysis for electric distributors in Ontario.
In addition, an example of the detailed calculations is provided in Appendix A of the report.
It is intended that addenda to the report will be posted on this Web site as on-going data analysis provides further insight.
Electric Distributors In Ontario
Prepared for Ontario Energy Board Staff
By F.J. Cronin, M. King and E. Colleran
PHB Hagler Bailly Consulting
July 6, 1999
1.0 - INTRODUCTION
Performance based regulation ("PBR") such as price caps has evolved over the last twenty years as a method to introduce and foster competitive behavior in sectors transitioning away from traditional approaches to regulating monopoly or contestable services. Price caps "control" prices rather than profits and loosen the ties between an individual utility's costs and rates. Price caps allow some flexibility with predetermined parameters and thus allow management to be more responsive to changing circumstances and market signals. Specifically, a price cap framework seeks to foster an environment where the benefits of competition can prevail while maintaining appropriate standards and protection for consumers and competitors from any potential monopoly rent seeking behavior of the incumbent utility.
PBR establishes benchmarks against which the incumbent utility must "compete" in determining its profit. Utilities that outperform the benchmarks have the potential for increased profits; utilities that underperform relative to the benchmarks have lower realized earnings. The level of the price cap over time then becomes critically important – too low and the incumbent utility is financially disadvantaged; too high and the incumbent firm will retain monopoly rents. Therefore, a central challenge for regulators and a continuing theme in the application of PBR is attempting to ensure that the economic drivers built into the design of the plan adequately balance these concerns. Careful consideration must ensure the appropriate specification of the cap formula and the correct measurement of relevant price and productivity indices.
As input to the Ontario Energy Board's ("OEB") PBR considerations, this report examines the economic operating performance of electric distribution utilities in Ontario over the 1988 to 1997 period. In particular, we estimate the change in total factor productivity ("TFP") and utility input prices. These historical calculations require extensive information on a number of items including the quantities and prices of inputs and outputs. With respect to inputs, data on all inputs have been collected; for one, capital, a twenty-year record of its components (i.e., book value, depreciation, additions and retirements) is necessary for consistency. Much of this information was provided by individual distribution utilities(1); other sources include the Municipal Electric Association, Statistics Canada and the Municipal Utility Databank (MUDBANK).
We find that on average, the typical electric distribution utility in Ontario had a growth in total factor productivity slightly less than one percent per year between 1988 and 1997. In fact, many utilities had growth in productivity significantly higher than the average: 40 percent of the utilities exceeded 1.25 percent and 18 percent exceeded 2 percent per year. We also estimate that the input price index for distribution utilities grew 1.4 percent per year including the price of line losses and about 1 percent excluding the price of line losses. During the same period, the CPI increased about 2.65 percent per year.
The remainder of this report is structured as follows: Section 2 discusses the theory and evolution of price cap regulation as it pertains to the specification of the rate adjustment formula, the associated economic parameters, and the effectiveness of implementation. Section 3 reviews the methodology, assumptions, and data involved in estimating total factor productivity and input prices. Section 4 presents the empirical results of our analysis for distribution utilities in Ontario. Appendix A presents an example of some detailed calculations for an individual utility. Appendix B lists utilities included in our analysis.
2.0 - THE THEORY AND EVOLUTION OF PRICE CAP REGULATION
The economic theory underpinning price caps relates the change in a firm's output price to the change in unit costs – i.e., the change in output price for a regulated utility equals the change in the utility's input prices minus the change in its productivity. Assuming no change in profit, this can be written as:
- dpu = dwu - dTFPu (1)
Where the d operator indicates annual percentage change, the superscript denotes the regulated utility, p is the relevant output price, w is the relevant input price, and TFP is the firm's total factor productivity.
In fact, the earliest major application of PBR employed the straightforward direct approach based on equation (1). In the decade of the 1980's, the U.S. Interstate Commerce Commission (ICC) successfully implemented price caps as a form of alternative regulation for major rail carriers in the U.S. The general price cap framework adopted and refined by the ICC between 1980 and 1989, directly measures changes in railroad unit costs in order to develop a maximum cap for regulated rail prices. Specifically, the calculation includes two components: the change in the railroad input price index (i.e., the "rail cost recovery index") minus the change in the railroad productivity index.
With respect to the cost recovery index, the ICC explicitly ruled out the use of readily available, aggregate measures of price escalation for the reason that such measures are too broad and "include many elements unrelated to rail costs."(2) Rather, an "all inclusive" index created by the American Association of Railroads, and modified by stakeholder inputs including federal and state governments, individual shippers and their associations, trade associations, and the ICC, was implemented in January 1985.(3) The index is a fixed- weight, input price index consisting of seven components. For example, the ICC specified depreciation as the measure of capital usage and indexed it to the Bureau of Labor Statistics producer price index for capital.
Some of the price cap plans put into effect since the ICC's PBR have relied on a variant of the equilibrium condition depicted in equation (1) that we might label the differential approach. Such an approach seeks to simplify the ongoing annual calculations for adjusting the cap by measuring industry performance relative to that of the aggregate economy as a whole over some historical period(4). Once certain relationships among prices and productivity at the aggregate economic level and the industry are estimated, the developers of the differential approach contend that the cap index can be updated by simply incorporating the most recent aggregate measure of price change.
In point of fact, many of the PBR applications based on a differential approach implemented before 1997 (e.g., the Federal Communications Commission in the U.S. for access charges, Oftel's in the U.K. for British Telecom,) resulted in rapid, pervasive and large increases in earnings for the incumbent firms due to mistakes in the PBR adjustment formula. Efforts to retain the differential approach by making it theoretically unbiased like the direct approach have now resulted in the need to include five adjustment parameters rather than the two in the direct approach. Since some of these adjustment parameters (e.g., aggregate TFP) may not be available for the past several years, the differential approach is forced to employ older data upon which to estimate its multiple differential relationships.
To see these relationships, recall equation (1) for an individual utility:
- dpu = dwu - dTFPu (1)
To derive the differential PBR formula, specify an aggregate version (A) of the equilibrium conditions as:
- dpA = dwA - dTFPA (2)
If we deduct equation (2) from equation (1)
We obtain:
- dpu - dpA = (dwu - dwA) - (dTFPu - dTFPA) (3A)
or
dpu = dpA + (dwu - dwA) - (dTFPu - dTFPA) (3B)
The term on the left-hand side of (3A) is the difference in output price changes between the utility and the aggregate economy. (pA could be represented by a relevant output price index issued by the government.) Equation (3A) thus states that the difference in output price changes is a function of two terms: the first representing the difference between input price changes between the utility and the aggregate economy; the second representing the difference between productivity changes between the utility and the aggregate economy.
In the applications of PBR by British regulators and by the FCC for the first ten years of alternative regulation, the first term on the right hand side of equation (3A) was not included. Utility input prices were growing more slowly then aggregate input prices, thus earnings tended to increase substantially for all utilities – not just those beating the productivity benchmark, i.e., dTFPu. In fact, dTFPu was also understated in many of these applications, in some cases being set below what turned out to be the historical average. Establishing the productivity factor so low reinforced the tendency for earnings to increase. As a result of these factors, regulators in the U.K. and the U.S. have responded to the unexpectedly sharp increase in earnings by instituting more frequent, detailed reviews than had been expected.(5) These reviews have usually resulted in regulators attempting to curtail the increase in earnings by raising the productivity differential between 100 and 150 percent.
Thus, prior PBR experiences with varying approaches to incorporating price and productivity in the price cap formula as well as theoretical considerations would seem to suggest that a direct approach would provide less risk (to both ratepayers and shareholders), more focused incentives, and the potential for a more effective PBR scheme. The direct approach, however, probably involves slightly more complicated update requirements. After considering these issues and the results discussed in Section 4, we recommend using a direct approach with a specific price index.
3.0 - ESTIMATING TOTAL FACTOR PRODUCTIVITY
Productivity represents the amount of output a particular firm can produce with a given amount of input. Changes in productivity are central to increasing living standards and maintaining stable price levels. Economists have developed comprehensive representations of productivity known as total factor productivity (TFP). It is TFP that has typically been employed in PBR. To measure TFP, we need to develop indexes for all outputs and inputs and corresponding weights with which to combine the output indexes into one and the input indexes into one. Productivity over time would then be measured by the ratio of outputs to input.
OUTPUTS
Output is represented as a weighted average of the number of customers by class(6) as the preferred output measure. In fact, number of customers was recommended by the OEB Cap Mechanism Task Force since it probably better reflects a "wires" only business.. Over history, it might be useful to also examine a measure based on energy. Thus, we also analyze a second measure based on kilowatt hours by class. Four classes are employed: residential, general service (i.e., under 5000 kW), large use (i.e., over 5000 kW) and street lighting(7). These variables are QRC, QGSC, QLUC and QSLC respectively, for number of customers and KWHR, KWHGS, KWHLU and KWHSL respectively, for kilowatt hours. These quantity indexes are weighted by revenue shares to aggregate to a total output index.
INPUTS
We calculate TFP based on a four-factor representation of inputs. These factors are capital, labor, materials, and line losses. For each input, we develop indexes of quantity and price as well as the share of total cost attributable to each input. Since the price of line losses will be recovered in the PBR through the on-going settlements process, we also estimate a three-factor input price index.
Capital
We employ a service price approach to capital costs. With this approach, the cost of capital in any year can be expressed as a function of a capital service price index and a capital quantity index. Thus:
- CKt = PKt x QKt (4)
Standard utility accounting of capital costs is based on book valuation (i.e., historical prices) and fails to reflect changing assets prices over time as a measure of input. Therefore, the capital quantity index is constructed using inflation – adjusted values for historical capital stock deployed before a benchmark year, as well as for subsequent additions and retirements. Both PK and QK require a measure of depreciation.
Deployed capital in distribution networks can and does last for many decades. In addition, distribution utilities have deployed capital at various times. Therefore, in constructing the capital quantity index we need to account for both these facts in order to consistently measure a utility's use of capital. Thus, we need to start (i.e., pick our benchmark year) decades ago to capture the deployment of capital accurately, to adjust capital deployed prior to our start date (i.e., our benchmark year) for asset price changes, and, to adjust subsequent additions and retirements for such changes in price.
We selected 1980 as our "benchmark year" based on a balancing of several considerations including data availability. The 1980 value of gross fixed assets is adjusted for accumulated depreciation to derive the undepreciated portion of deployed capital valuated in the dollars of its year of acquisition. Real stock in 1980 (i.e., constant dollar capital) is estimated by deflating the undepreciated capital in 1980 by a capital asset price constructed by "triangularizing" the pre-benchmark asset prices to create a weighted average asset price for assets deployed during the twenty years before our benchmark (i.e., from 1960 to 1979). This triangularized weight gives greater weight to more recent capital additions since these assets should comprise a greater share of the book value of capital(8). The capital asset price index, CAP, is the electric utility distribution investment price index published by Statistics Canada.
Subsequent (i.e., post-benchmark) values of the capital quantity index are expressed as a perpetual inventory model:
- QKt = (1-d) (QKt-1 + AKt - Rt ) (5)
CAPt CAPt-n
The capital service price index, PK is:
- PKt = (rt + d) CAPt (6)
r is the Canadian long bond rate, a measure of opportunity cost.
Labour
Labour costs, CL, include all non-capitalized wages, salaries, payroll taxes and fringe for a utility's own employees. Total compensation was reported by utilities on the survey. Total compensation was adjusted for capitalized labour which is included in CAP, QK and AK. Data from a dozen utilities was examined to develop an estimate of capitalized labour. For this calculation we have assumed 15 percent of labour is capitalized. Adjusted compensation is the expenditure employed in developing the input weight. We measure the quantity of labour, QL, by the number of full-time employees. The price of labour, PL, is represented for each utility by its line crew wage rate. This data is compiled by the Municipal Electric Association.
Materials
Material inputs are all inputs excluding capital, utility labor and line losses. Material costs, CM, are calculated as the non-labor cost portion of three operating accounts: operating and maintenance, billing and collecting, and administration. Data from a dozen utilities of varying size was examined to develop "typical" splits between utility labor and material charged to these accounts. We found that about 35 percent of expenditures in these accounts represent materials (e.g., services, materials expensed purchases, contract labor). We estimate each utility's material costs by applying this ratio to its reported expenditures in the Ontario Hydro Statistical Yearbook(9). The price of materials, PM, is represented by the Industrial Producer Price Index published by Statistics Canada. Material inputs are obtained by calculating the constant dollar expenditure, QM, derived by deflating CM by PM.
Line Losses
The cost of line losses, CLL, is calculated based on reported line losses, QLL, from the task force survey and the price of purchased power, PPP. In the event that this data was not reported, we calculated these data from information in the MUDBANK.
TOTAL FACTOR PRODUCTIVITY AND THE INPUT PRICE INDEX
Generally, a TFP index can be specified as:
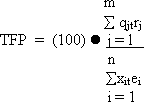 (7)
(7)where the index includes the outputs qj (i.e., QRC, QGSC, QLUC, QSLC) and the input xi (i.e., QK, QL, QM and QLL). Weights are based on revenue shares for outputs rj and cost shares for inputs, ei.
Similarly, an input price index (IPI) can be specified as :
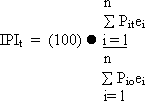 (8)
(8)where the index includes PK, PL, PM and PPP in the four-factor case or only the first three in the three-factor case.
Economists have employed increasingly refined and complex representations with respect to the form of equations (7) and (8) and their calculated growth rate. For example, much of the work on price indexes has relied on such forms as Paasche or Laspeyres to represent the weights. In the latter, weights are fixed on a base or other given-year expenditure. This choice of fixed weights greatly simplifies the calculation and reduces the knowledge requirement on the part of the reader relative to some other choices with much more complicated representations (e.g., geometric weighting of the mean of two alternative forms) – particularly, if one also employs a chained calculation (i.e., a calculation which links each two-year period sequentially).
Because this document is meant to serve as a primer and reference to more than 250 Ontario distribution utilities of varying sizes from several hundred customers to almost a million, and because the weights calculated are relatively stable, we have chosen to present our calculations based on a fixed mid-point weighting scheme (i.e., 1993)(10). Alternative assumptions are examined and reported. We believe that the findings reported below would not materially be affected by altering these choices. In terms of the average TFP and IPI indexes, we report growth both as the average annual growth from start point to end point and that based on the more mathematically precise logarithmic calculation, since we felt that transparency and ease of understanding were critical. Conclusions drawn regarding TFP and the IPI and all other calculations are based on the latter approach.
4.0 - FINDINGS
This section presents the results of our analysis with respect to TFP and the input price index for electric distribution utilities in Ontario. Results are based on data from 40 utilities ranging in size from less than 800 to more than 200,000 customers.(11) Results of calculations for alternative assumptions are also presented.
Originally, yardstick competition was one form of PBR considered for use in Ontario. This type of PBR in which a peer group of utilities "competes" against a benchmark (i.e., yardstick such as average total cost per customer) among the utilities has several attractive features (e.g., the utilities' actual performance determines the benchmark and the competition among utilities tends to mimic a competitive market process). Unfortunately, the data were not sufficiently standardized to permit adjustments to observed historical results for factors beyond management's control. Since total cost per customer has a wide range across all size categories, without such adjustments, some utilities might be disadvantaged.
Table 4.1 presents average total cost per customer by utility size class. Note that the mean increases from $385 for the small utilities to $484 for the medium and to $504 for the large. Furthermore, note that the range also increases from $291 for the small utilities to $312 for the medium to $731 for the large.
Average Total Cost Per Customer and
Range from Minimum to Maximum by Size Class*
| Sample Size | Mean | Range | |
| Large | 12 | 504 | 731 |
| Medium | 15 | 484 | 312 |
| Small | 13 | 385 | 291 |
* Small utilities have less than 10,000 customers, medium between 10,000 and 50,000, and large more than 50,000.
Based on these considerations, a price cap framework was recommended by the OEB task forces. In fact, embedded in the price cap plan are important yardstick features, i.e., rather than compete on total cost per customer, utilities compete on changes in input prices and TFP. These latter benchmarks, in fact, determine changes in cost. Thus, by calculating an average across utilities for these economic parameters we are actually blending these important yardstick features into the price cap PBR.
TOTAL FACTOR PRODUCTIVITY
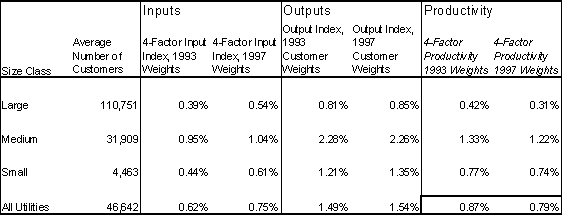
Table 4.2 presents the results of our analysis on TFP by size class. Results for two weighting schemes are shown. Looking at the results based on 1993 weights, we see that the average change in TFP among utilities is 0.87 percent per year. Results range from 0.42 percent for large, to 0.77 percent for small, to 1.33 percent for medium. Results using 1997 weights are slightly lower but comparable in magnitude and pattern.
Among individual utilities, 21 had growth in TFP greater than 1.0 percent per year; 16 growth greater than 1.25; 14 growth greater than 1.5; and, 7 had growth greater than 2.0. These results are based on the 1993 weights.
Productivity Analysis by Customer Size Class
10-year percent Change
INPUT PRICE INDEX
Table 4.3 presents the results of our analysis on the input price index for electric distribution utilities in Ontario. This table shows results for alternative weights by utility size class. Both four-factor and three-factor index results are presented.
Observe that the overall mean with four factors and 1993 weights is 1.42 percent. Results by size class range from 1.30 to 1.54. Note that the range of results increases from large to medium to small. Also we can see that the results based on three other weighting schemes (i.e; 1988, 1997, or interval average) are generally quite similar.
Going forward, the price of line losses will be embedded in the monthly settlements process – not recovered through the PBR input price index as it has been in the past. We therefore calculate a three-factor input price index. Results using 1993 weights are shown in Table 4.3. Note that the overall mean is now 0.96 percent per year with a corresponding fall in the class averages of a similar one-third from the four-factor index.
Input Price Index Results – 1988 -1997
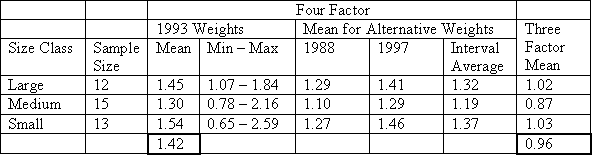
Table 4.4 presents the 1993 weights for the typical utility for both the three and four- factor cases. Typical weights by size class are also shown. On average, about 45 percent of a typical utility's total cost is related to capital. Remaining cost shares are 29 percent for labor, 13 for material and 13 for line losses. Medium sized utilities tend to have a slightly higher share for capital and slightly lower shares for labour and material. In the three-factor case the cost shares are 52 percent for capital, 34 percent for labour, and 15 for materials.(12)
1993 Average Weights for Cost Shares
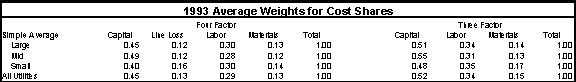
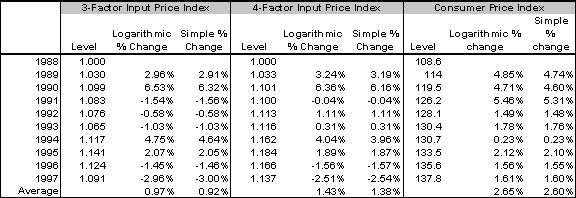
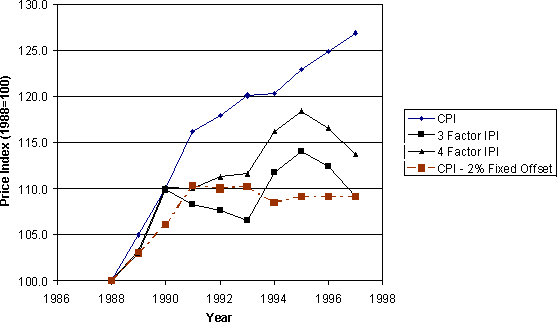
Table 4.5 presents the input price index and the CPI over the 1988 to 1997 period. Note that in logarithmic change terms, the CPI grows on average 2.65 percent – 1.22 percent higher per year than the four-factor's growth of 1.43 per year and 1.68 percent higher per year than three-factor's growth of .97 percent. Figure 4.1 presents the results of adjusting the CPI by the average 10 year difference between the CPI and the input price index so that we forced the two series to be equal in the tenth year. Note that the resulting adjusted CPI series, even though it is set to equal the IPI in this tenth year, still does a poor job tracking the input price index between the standard and points.
Input Price Index and CPI: 1988 to 1997
Cumulative Price Indeces
Return to previous page
(1) For a copy of this survey instrument, see the Report of the Ontario Energy Board Cap Mechanism Task Force, May 1999.
Return
(2) Interstate Commerce Commission, ExParte No. 290 (November, 1980), p.3.
Return
(3) Ex Parte No. 290 (January, 1985), p.7.
Return
(4) Early discussions of PBR in the 1980s and early 1990s sometimes considered employing an aggregate price index like the CPI as a substitute for the industry input price. However, the former is an output price representing consumers' purchases while the latter is an input price reflecting a specific industry's purchases. The composition of the two are markedly different. Even if one adjusts the CPI to track the input price index on average over some historical comparison period, that does not guarantee that the input price and adjusted CPI would track over subintervals. Nor does an average adjustment equating the two prices over the historical period mean that over the future course of the PBR and the relationships underlying the adjustment would remain constant – particularly when the input price index would have a weight of 40 to 50 percent on capital.
Return
(5) This is not meant to imply that the observed increase in earnings was not based also on improvements in business operations undertaken by management in response to the incentives.
Return
(6) Connected services are probably a better term since some connected sites can have multiple dwellings.
Return
(7) The inclusion or exclusion of street lighting did not significantly affect the results.
Return
(8) This weighting scheme gives a weight of 0.5 percent to the 1960 asset price and a weight of 9.5 percent to the 1979 asset price. This calculation revalues 1980 undepreciated assets by about 150 percent.
Return
(9) Since PM and PL grow similarly over the 1988 to 1997 period, the assumed split between labor and materials does not materially affect the results.
Return
(10) Some PBR applications have chosen to employ fixed weights and some the more complex schemes.
Return
(11) Utilities included in our sample are listed in Appendix B.
Return
(12) These weights are generally consistent with weights reported from utilities in other jurisdictions.
Return
Return to previous page